Adam Lipowski
Algorytmy genetyczne
Carver Mead: engineers would be foolish to ignore the lessons of a billion years of evolution
Carver Mead: engineers would be foolish to ignore the lessons of a billion years of evolution
Ewolucja biologiczna w
'pigułce'
Długotrwałe poddawanie populacji mechanizmom ewolucji powoduje stopniowe udoskonalenie należących do niej osobników.
Genotyp - ciąg symboli kodujących kompletny zestaw cech osobnika. W przypadku istot żywych jest to DNA (lub RNA w przypadku wirusów).
Fenotyp - zbiór cech osobnika odpowiadający danemu genotypowi.
Populacja - zbiór osobników (fenotypów), żyjących w danym środowisku, oddziałujących ze sobą i rozmnażających się i umierających.
Mechanizmy ewolucji:
a) Wariacja - mechanizm powodujący zwiększanie różnorodności populacji

b) Selekcja - mechanizm powodujący zmniejszanie różnorodności populacji.
Algorytmy genetyczne
W latach 60-tych pojawiły sie programy wykorzystujące główne idee ewolucji biologicznej. Od tego czasu datuje się ich burzliwy rozwój i obecnie znajdują one liczne zastosowania w technice, medycynie czy informatyce. Szczególnie użyteczne są one do rozwiązywania (zwykle przybliżonego) złożonych problemów optymalizacyjnych.
Ideą algorytmu genetycznego jest wyłonienie osobnika (tj. programu, metody) który jest najlepiej przystosowany. Stopień przystosowania określa tzw. funkcja celu (zwana niekiedy funkcją przystosowania). Osobniki radzące sobie lepiej (mające większą wartość funkcji celu) wydają więcej potomstwa (do nich zbliżonego).
Metody znajdowania optymalnych rozwiązań:
- analityczne (gradientowe, znajdują rozwiązania lokalne)
- przeglądowe (np., przejrzenie tablicy warotści funkcji; dla wielu zastosowań nieefektywne)
- losowe (algorytmy genetyczne, symulowane wyżarzanie, algorytmy mrówkowe,...)
Schemat algorytmu genetycznego
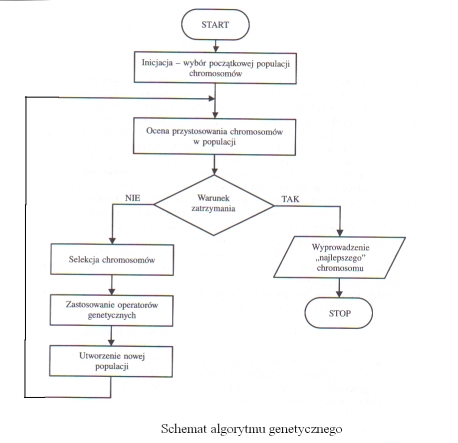
W literaturze wyróżnia się algorytmy genetyczne oraz ewolucyjne. W tych pierwszych istotniejszą rolę odgrywa krzyżowanie a w drugich zmienność jest realizowana zwykle poprzez mutacje. Algorytmy ewolucyjne używają zwykle bardziej bezpośrednich reprezentacji modelu i operatory mutacji często działają na fenotypach. W algorytmach genetycznych istotna jest binaryzacja genotypu (operatory krzyżowania i mutacji działają na genotypach). Ponadto, pewne zbliżone techniki określane są mianem programowania genetycznego/ewolucyjnego.
Niekiedy stosuje się strategie, które są połączeniem kilku metod, np. symulowane wyżarzanie i programowanie genetyczne.
Łączy się również programowanie gentyczne z przeszukiwaniem lokalnym (Lamarkizm).
Przykład-1: Znajdź maximum funkcji np. f(x) = -x+4-1/x gdzi 0<x<3.
Osobniki to liczby z przedziału (0,3) w zapisie binarnym. Funkcją celu jest f(x). Początkowa populacja liczb podlega rozmnażaniu (z mutacją i krzyżowaniem) i selekcją.Można stosować dwa rodzaje selekcji. Selekcja twarda: lepszy przeżywa. gorszy umiera. Selekcja miękka: słabsze osobniki też mogą przeżywać i się rozmnażać lecz z mniejszym prawdopodobieństwem.
Iterowany dylemat więznia to również pewien algorytm genetyczny (funkcją celu jest uzyskany wynik). Można rozpatrzeć np strategie z dłuższą pamięcią.
Przykład-2: Znajdź tekst (słowo).
1) Poszukiwanie losowe (aplet) .
2. Poszukiwanie z funkcją przystosowania f(s)=m/n gdzie: s - łańcuch o długości n mający m liter zgodnych z poszukiwanym łańcuchem (aplet). Najpierw generowana jest pewna populacja początkowa. Następnie połowę najgorzej przystosowanych osobników odrzucamy a na ich miejsce każdy przeżywający osobnik tworzy punktowo zmutowanego potomka. Procedurę kontynuujemy aż do znalezienia łańcucha o f(s)=1.
Odwrotność funkcji przystosowania jest niekiedy nazywana funkcją kosztu. Dla słów dwuliterowych funkcja kosztu odpowiadająca funkcji f(s) ma następujący kształt (minimum funkcji kosztu to zarazem maksimum przystosowania)
Wprowadzając pojęcie odległości między literami jako kwadrat różnicy liczb odpowiadających pozycjom liter w alfabecie, funkcję kosztu można zdefiniować następująco:
gdzie si i wi to liczby odpowiadające i-tym literom w osobniku s i wzorcu w.
Np. dla s=pył, w=rum mamy koszt(s)=1+4+1=6.
Dla słów dwuliterowych koszt(s) może wyglądać następująco:
Mimo, że minimum obu funkcji przypada w tym samym miejscu (a więc algorytm znajdzie w obu przypadkach te same rozwiązania) ich kształt jest istotnie różny. Niekiedy wybór przystosowania lub kosztu może mieć wpływ na efektywność algorytmu genetycznego.
Pewną odmianą omawianych strategii optymalizacyjnych są algorytmy mrówkowe. Podstawą tych algorytmów jest obserwacja, iż mrówki tworzą i podążają szlakiem feromonowym. Ponieważ feromony ulatniają się z upływem czasu ścieżki najkrótsze mają największe szanse na ponowną trawersację przez inne (lub powracające) mrówki i ich 'waga' wzrasta. Algorytmy mrówkowe były wykorzystywane do wielu zadań optymalizacyjnych takich jak: problem komiwojażera, kolorowanie grafu, planowanie przejazdu, porządkowanie, etc. Zachowanie innych owadów społecznych (pszczoły, termity) również bywa inspiracją do budowy pewnych systemów obliczeniowych (Bonabeau, Theraulaz, Mądrości Roju, Świat Nauki nr 6, 49 (2000)).
Pojęcie roju odgrywa istotną rolę w poszukiwaniach samo-naprawiającch się systemów obliczeniowych (wadliwy/zainfekowany element jest usuwany i zastępowany przez sprawny). Przy tworzeniu takich samo-naprawiających systemów pomocne są również pewne cechy układu immunologicznego:
Inne przykłady
Literatura:
- Z.Michalewicz , Algorytmy genetyczne + struktury danych = programy ewolucyjne, (WNT, 1996)
- I. Białynicki-Birula i I.Białynicka-Birula, Modelowanie reczywistości, (Prószyński i S-ka, 2002).
- E. Bonabeau, M.Dorigo & G.Theraulaz, 'Inspiration for optimization from social insect behaviour', Nature 406, p.39 (2000).
- L. Rutkowski, Metody i techniki sztucznej inteligencji, PWN 2005
Problem 1. Uogólnij program z przykładu 2 tak aby można było wprowadzać tekst złożony z kilku słów.
Problem 2. Innym sposobem implementacji rankingu jest tzw. selekcja konkursowa. Wybierz losowo dwóch osobników: zwycięzca rozmnaża się a pokonany ginie. Kontynuuj aż do utworzenia N nowych osobników.
Problem 3. Zagadnienie podziału zbioru liczb.
Niech dany będzie zbiór liczb x_1,x_2,...x_n. Znajdź podział tego zbioru na dwa podzbiory i takie, że sumy liczb w każdym podzbiorze są równe (lub minimalnie różne).
Na przykład (3,4,4,7,8,10,11,14,22,27) można podzielić na (3,4,7,14,27) i (4,8,10,11,22).
Jak zdefiniowany jest osobnik w tym zagadnieniu? Zbadaj jak rozwiązywalność tego zadania zależy od zakresu liczb L (0<x_i<L).
Przybliżona argumentacja (Gent & Walsh, 1996): Prawdopodobieństwo, że jedna z cyfr (w zapisie binarnym) sumy pokrywa się z poprawną wartością wynosi 1/2. Ponieważ cyfr jest log2(L) więc prawdopodobieństwo, że przypadkowy podział jest poprawny wynosi 1/(2^(log2(L)))=1/L. Liczba rozwiązań Sol wynosi więc Sol=2^n/L (dla Sol<1 zagadnienie nie ma rozwiązań). Można pokazać, że w granicy nieskończenie dużego n dla Sol=1 w zagadnieniu tym pojawia się przejście fazowe między przypadkiem łatwym (bardzo wiele rozwiązań) i (zwykle) nierozwiązywalnym.
Różnica sum podzbiorów zwykle mocno zależy od tego jak wybraliśmy te podzbiory
Istnieje wiele heurystyk (innych niż algorytmy genetyczne) rozwiązujących problem podziału liczb. Przykładem mogą być algorytmy: zachłanny oraz Karmarkar'a-Karp'a
Problem podziału liczb należy do klasy problemów NP. Oznacza to, że znalezienie rozwiązania w tym przypadku wymaga (najprawdopodobniej) wykładniczego, w funkcji liczebności wyjściowego zbioru n, czasu obliczeń, jednak sprawdzenie czy pewien podział spełnia warunki zadania da się wykonać w czasie wielomianowym (względem n).
Algorytmy zachłanny lub Karmarkar'a-Karp'a mają wielomianowy czas działania, jednakże zwykle nie znajdują one najlepszego rozwiązania.
Problem spełnialności
Innym przykładem zagadnienia optymalizacyjnego, w którym pojawia się przejście fazowe jest problem spełnialności (SAT), gdzie poszukiwane są wartości zmiennych boolowskich, dla których prawdziwe będzie dane wyrażenie (koniunkcja alternatyw). Np. (x||y)&&(!x||!y)&&(x||z) jest prawdziwe dla x=false, y=true i z=true.Gdy liczba zmiennych boolowskich oraz złożoność wyrażenia wzrasta, wyznaczenie wartościowania dla którego to wyrażenie jest prawdziwe może być dość skomplikowane. W zagadnieniu tym (podobnie jak w problemie podziału zbioru liczb) może pojawić się przejście fazowe separujące dwa obszary:
(I) faza gdzie dość łatwo można znaleźć rozwiązanie (więcej zmiennych niż klauzul (under-constrained) budujących rozpatrywane wyrażenie; łatwo więc znaleźć wartościowanie zmiennych, dla którego wyrażenie będzie prawdziwe)
(II) faza gdzie dość łatwo pokazać, że rozwiązanie nie istnieje (zbyt mało zmiennych a zbyt dużo warunków do spełnienia (over-constrained)).
Parametrem kontrolnym (określającym to w jakiej fazie się znajdujemy) może być iloraz liczby klauzul do ilości zmiennych.
W punkcie przejścia fazowego rozstrzygnięcie czy istnieje rozwiązanie jest zwykle bardzo trudne. Więcej na ten temat: R. Monasson et al., Determining computational complexity from characteristic `phase transitions', Nature vol. 400, str.133 (1999).
W literaturze rozważa się tzw. problem K-SAT gdzie K jest ilością zmiennych budujących klauzulę. Problemy 1-SAT i 2-SAT są rozwiązywalne w czasie wielomianowym natoomiast dla K>2 K-SAT jest problemem NP-zupełnym. Oznacza to, że jeżeli dla tego problemu znaleziony by został algorytm wielomianowy, to za jego pomocą udałoby się rozwiązać również wiele innych problemów klasy NP.
Zadanie: Opracuj algorytm genetyczny rozwiązujący 2-SAT
Długotrwałe poddawanie populacji mechanizmom ewolucji powoduje stopniowe udoskonalenie należących do niej osobników.
Genotyp - ciąg symboli kodujących kompletny zestaw cech osobnika. W przypadku istot żywych jest to DNA (lub RNA w przypadku wirusów).
Fenotyp - zbiór cech osobnika odpowiadający danemu genotypowi.
Populacja - zbiór osobników (fenotypów), żyjących w danym środowisku, oddziałujących ze sobą i rozmnażających się i umierających.
Mechanizmy ewolucji:
a) Wariacja - mechanizm powodujący zwiększanie różnorodności populacji
- mutacja - przypadkowa, częściowa zmiana genotypu danego osobnika.
- krzyżowanie - powstawanie nowego genotypu na drodze połączenia dwóch istniejących już w populacji genotypów

b) Selekcja - mechanizm powodujący zmniejszanie różnorodności populacji.
- selekcja naturalna - zjawisko polegające na wymieraniu tych osobników, które są gorzej przystosowane do środowiska.
- selekcja płciowa - produkcja większej liczby potomostwa przez osobniki lepiej przystosowane.
Algorytmy genetyczne
W latach 60-tych pojawiły sie programy wykorzystujące główne idee ewolucji biologicznej. Od tego czasu datuje się ich burzliwy rozwój i obecnie znajdują one liczne zastosowania w technice, medycynie czy informatyce. Szczególnie użyteczne są one do rozwiązywania (zwykle przybliżonego) złożonych problemów optymalizacyjnych.
Ideą algorytmu genetycznego jest wyłonienie osobnika (tj. programu, metody) który jest najlepiej przystosowany. Stopień przystosowania określa tzw. funkcja celu (zwana niekiedy funkcją przystosowania). Osobniki radzące sobie lepiej (mające większą wartość funkcji celu) wydają więcej potomstwa (do nich zbliżonego).
Metody znajdowania optymalnych rozwiązań:
- analityczne (gradientowe, znajdują rozwiązania lokalne)
- przeglądowe (np., przejrzenie tablicy warotści funkcji; dla wielu zastosowań nieefektywne)
- losowe (algorytmy genetyczne, symulowane wyżarzanie, algorytmy mrówkowe,...)
Schemat algorytmu genetycznego

W literaturze wyróżnia się algorytmy genetyczne oraz ewolucyjne. W tych pierwszych istotniejszą rolę odgrywa krzyżowanie a w drugich zmienność jest realizowana zwykle poprzez mutacje. Algorytmy ewolucyjne używają zwykle bardziej bezpośrednich reprezentacji modelu i operatory mutacji często działają na fenotypach. W algorytmach genetycznych istotna jest binaryzacja genotypu (operatory krzyżowania i mutacji działają na genotypach). Ponadto, pewne zbliżone techniki określane są mianem programowania genetycznego/ewolucyjnego.
Niekiedy stosuje się strategie, które są połączeniem kilku metod, np. symulowane wyżarzanie i programowanie genetyczne.
Łączy się również programowanie gentyczne z przeszukiwaniem lokalnym (Lamarkizm).
Przykład-1: Znajdź maximum funkcji np. f(x) = -x+4-1/x gdzi 0<x<3.
Osobniki to liczby z przedziału (0,3) w zapisie binarnym. Funkcją celu jest f(x). Początkowa populacja liczb podlega rozmnażaniu (z mutacją i krzyżowaniem) i selekcją.Można stosować dwa rodzaje selekcji. Selekcja twarda: lepszy przeżywa. gorszy umiera. Selekcja miękka: słabsze osobniki też mogą przeżywać i się rozmnażać lecz z mniejszym prawdopodobieństwem.
Iterowany dylemat więznia to również pewien algorytm genetyczny (funkcją celu jest uzyskany wynik). Można rozpatrzeć np strategie z dłuższą pamięcią.
Przykład-2: Znajdź tekst (słowo).
1) Poszukiwanie losowe (aplet) .
2. Poszukiwanie z funkcją przystosowania f(s)=m/n gdzie: s - łańcuch o długości n mający m liter zgodnych z poszukiwanym łańcuchem (aplet). Najpierw generowana jest pewna populacja początkowa. Następnie połowę najgorzej przystosowanych osobników odrzucamy a na ich miejsce każdy przeżywający osobnik tworzy punktowo zmutowanego potomka. Procedurę kontynuujemy aż do znalezienia łańcucha o f(s)=1.
Odwrotność funkcji przystosowania jest niekiedy nazywana funkcją kosztu. Dla słów dwuliterowych funkcja kosztu odpowiadająca funkcji f(s) ma następujący kształt (minimum funkcji kosztu to zarazem maksimum przystosowania)

Wprowadzając pojęcie odległości między literami jako kwadrat różnicy liczb odpowiadających pozycjom liter w alfabecie, funkcję kosztu można zdefiniować następująco:
gdzie si i wi to liczby odpowiadające i-tym literom w osobniku s i wzorcu w.
Np. dla s=pył, w=rum mamy koszt(s)=1+4+1=6.
Dla słów dwuliterowych koszt(s) może wyglądać następująco:

Mimo, że minimum obu funkcji przypada w tym samym miejscu (a więc algorytm znajdzie w obu przypadkach te same rozwiązania) ich kształt jest istotnie różny. Niekiedy wybór przystosowania lub kosztu może mieć wpływ na efektywność algorytmu genetycznego.
Pewną odmianą omawianych strategii optymalizacyjnych są algorytmy mrówkowe. Podstawą tych algorytmów jest obserwacja, iż mrówki tworzą i podążają szlakiem feromonowym. Ponieważ feromony ulatniają się z upływem czasu ścieżki najkrótsze mają największe szanse na ponowną trawersację przez inne (lub powracające) mrówki i ich 'waga' wzrasta. Algorytmy mrówkowe były wykorzystywane do wielu zadań optymalizacyjnych takich jak: problem komiwojażera, kolorowanie grafu, planowanie przejazdu, porządkowanie, etc. Zachowanie innych owadów społecznych (pszczoły, termity) również bywa inspiracją do budowy pewnych systemów obliczeniowych (Bonabeau, Theraulaz, Mądrości Roju, Świat Nauki nr 6, 49 (2000)).
Pojęcie roju odgrywa istotną rolę w poszukiwaniach samo-naprawiającch się systemów obliczeniowych (wadliwy/zainfekowany element jest usuwany i zastępowany przez sprawny). Przy tworzeniu takich samo-naprawiających systemów pomocne są również pewne cechy układu immunologicznego:
- brak centralnego sterowania
- różnorodność systemów operacyjnych lub architektury
- autonomiczność (automatyczna likwidacja uszkodzenia)
- pewna tolerancja błędu
- adaptatywny
- niedoskonały (wykrywający pewną grupę
wirusów a nie jego jeden rodzaj)
Inne przykłady
Literatura:
- Z.Michalewicz , Algorytmy genetyczne + struktury danych = programy ewolucyjne, (WNT, 1996)
- I. Białynicki-Birula i I.Białynicka-Birula, Modelowanie reczywistości, (Prószyński i S-ka, 2002).
- E. Bonabeau, M.Dorigo & G.Theraulaz, 'Inspiration for optimization from social insect behaviour', Nature 406, p.39 (2000).
- L. Rutkowski, Metody i techniki sztucznej inteligencji, PWN 2005
Problem 1. Uogólnij program z przykładu 2 tak aby można było wprowadzać tekst złożony z kilku słów.
Problem 2. Innym sposobem implementacji rankingu jest tzw. selekcja konkursowa. Wybierz losowo dwóch osobników: zwycięzca rozmnaża się a pokonany ginie. Kontynuuj aż do utworzenia N nowych osobników.
Problem 3. Zagadnienie podziału zbioru liczb.
Niech dany będzie zbiór liczb x_1,x_2,...x_n. Znajdź podział tego zbioru na dwa podzbiory i takie, że sumy liczb w każdym podzbiorze są równe (lub minimalnie różne).
Na przykład (3,4,4,7,8,10,11,14,22,27) można podzielić na (3,4,7,14,27) i (4,8,10,11,22).
Jak zdefiniowany jest osobnik w tym zagadnieniu? Zbadaj jak rozwiązywalność tego zadania zależy od zakresu liczb L (0<x_i<L).
Przybliżona argumentacja (Gent & Walsh, 1996): Prawdopodobieństwo, że jedna z cyfr (w zapisie binarnym) sumy pokrywa się z poprawną wartością wynosi 1/2. Ponieważ cyfr jest log2(L) więc prawdopodobieństwo, że przypadkowy podział jest poprawny wynosi 1/(2^(log2(L)))=1/L. Liczba rozwiązań Sol wynosi więc Sol=2^n/L (dla Sol<1 zagadnienie nie ma rozwiązań). Można pokazać, że w granicy nieskończenie dużego n dla Sol=1 w zagadnieniu tym pojawia się przejście fazowe między przypadkiem łatwym (bardzo wiele rozwiązań) i (zwykle) nierozwiązywalnym.

Różnica sum podzbiorów zwykle mocno zależy od tego jak wybraliśmy te podzbiory

Istnieje wiele heurystyk (innych niż algorytmy genetyczne) rozwiązujących problem podziału liczb. Przykładem mogą być algorytmy: zachłanny oraz Karmarkar'a-Karp'a

Problem podziału liczb należy do klasy problemów NP. Oznacza to, że znalezienie rozwiązania w tym przypadku wymaga (najprawdopodobniej) wykładniczego, w funkcji liczebności wyjściowego zbioru n, czasu obliczeń, jednak sprawdzenie czy pewien podział spełnia warunki zadania da się wykonać w czasie wielomianowym (względem n).
Algorytmy zachłanny lub Karmarkar'a-Karp'a mają wielomianowy czas działania, jednakże zwykle nie znajdują one najlepszego rozwiązania.
Problem spełnialności
Innym przykładem zagadnienia optymalizacyjnego, w którym pojawia się przejście fazowe jest problem spełnialności (SAT), gdzie poszukiwane są wartości zmiennych boolowskich, dla których prawdziwe będzie dane wyrażenie (koniunkcja alternatyw). Np. (x||y)&&(!x||!y)&&(x||z) jest prawdziwe dla x=false, y=true i z=true.Gdy liczba zmiennych boolowskich oraz złożoność wyrażenia wzrasta, wyznaczenie wartościowania dla którego to wyrażenie jest prawdziwe może być dość skomplikowane. W zagadnieniu tym (podobnie jak w problemie podziału zbioru liczb) może pojawić się przejście fazowe separujące dwa obszary:
(I) faza gdzie dość łatwo można znaleźć rozwiązanie (więcej zmiennych niż klauzul (under-constrained) budujących rozpatrywane wyrażenie; łatwo więc znaleźć wartościowanie zmiennych, dla którego wyrażenie będzie prawdziwe)
(II) faza gdzie dość łatwo pokazać, że rozwiązanie nie istnieje (zbyt mało zmiennych a zbyt dużo warunków do spełnienia (over-constrained)).
Parametrem kontrolnym (określającym to w jakiej fazie się znajdujemy) może być iloraz liczby klauzul do ilości zmiennych.
W punkcie przejścia fazowego rozstrzygnięcie czy istnieje rozwiązanie jest zwykle bardzo trudne. Więcej na ten temat: R. Monasson et al., Determining computational complexity from characteristic `phase transitions', Nature vol. 400, str.133 (1999).
W literaturze rozważa się tzw. problem K-SAT gdzie K jest ilością zmiennych budujących klauzulę. Problemy 1-SAT i 2-SAT są rozwiązywalne w czasie wielomianowym natoomiast dla K>2 K-SAT jest problemem NP-zupełnym. Oznacza to, że jeżeli dla tego problemu znaleziony by został algorytm wielomianowy, to za jego pomocą udałoby się rozwiązać również wiele innych problemów klasy NP.
Zadanie: Opracuj algorytm genetyczny rozwiązujący 2-SAT